I Numeri Interi Relativi
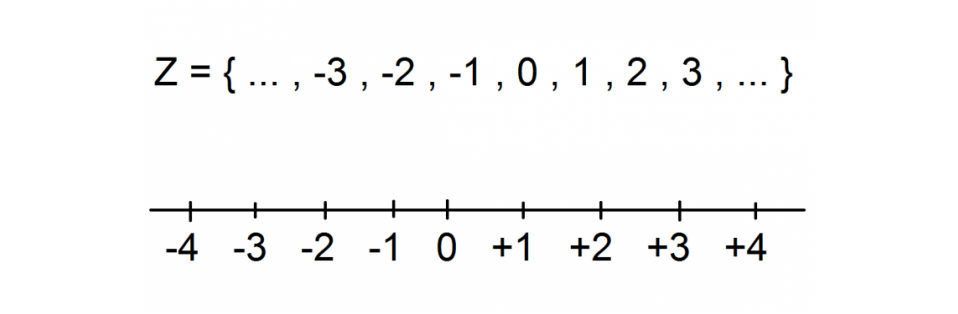
I Numeri Interi sono i Numeri che impariamo da piccoli a contare, sommare o restare.
Cosa sono I Numeri Interi Relativi ?
I Numeri Interi sono quelli più usati. Fanno parte di questi, tutti i numeri naturali, il zero e i suoi negativi. Questo insieme di Numeri Interi hanno un simbolo che li rappresenta, la lettera Z, chiamata ZHALEM, in lingua tedesca.
Tutto l’insieme di Numeri Interi: ℤ = {…−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 …}
I Numeri Interi sulla retta numerica

Da sempre utilizziamo la retta numerica per poter inserire i Numeri Interi di forma grafica. Questa immagine si rappresenta con una linea retta dove nel punto centrale si trova il numero zero. Poi le due metà sono simmetriche e arrivano fino l’infinito.
Nel lato sinistro ci sono in rosso i Numeri Negativi che iniziano per -1 e continuano:-2, -3,-4 e cosi fino l’infinito. Invece nella zona destra, in azzurro, troviamo i Numeri Positivi, che non hanno bisogno del simbolo della somma. Comunque non è errato scrivere il simbolo + quando parliamo di Numeri Interi Positivi, solo che non e necessario.
Il segno nei Numeri Interi
Come ti abbiamo mostrato sulla retta numerica, i Numeri Interi sono caratterizzati da un segno positivo o negativo ( + o -).
– L’unico segno obbligatorio e quello – , che ci indica quando un Numero e Negativo. In matematica la presenza o no del segno – cambia completamente l’uso del numero. Quando un numero e Negativo ( -2 ) lo leggiamo “meno due”.
– Il segno + non e necessario usarlo, pero la sua presenza ci aiuta e non è un errore utilizzarlo.
– Il numero zero non ha bisogno di nessun segno.
Proprietà dei Numeri Interi Relativi
La struttura algebraica che formano i Numeri Interi a traverso la moltiplicazione e la somma e conosciuta con il nome di anello.
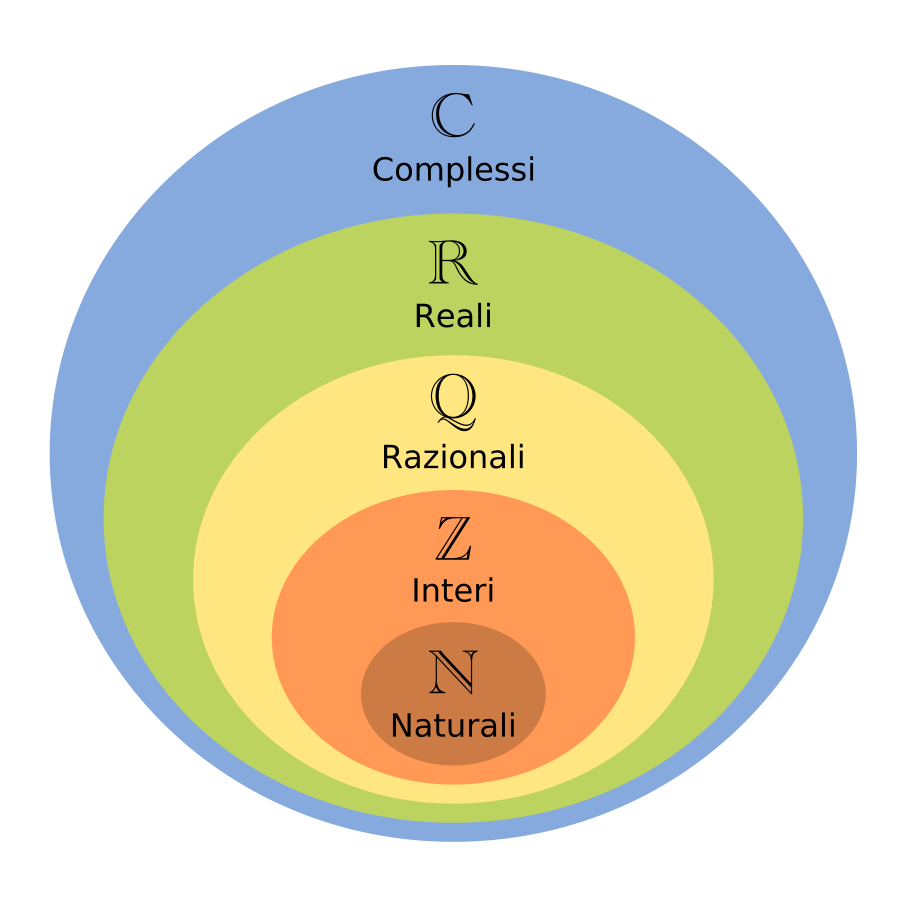
I Numeri Interi Relativi fanno parte della famiglia dei Numeri Razionali come puoi vedere nel diagramma di Eulero-Venn. Puoi osservare nello stesso diagramma che i Numeri Naturali provengono dei Numeri Interi i quali hanno una struttura ordinata ed infinita in entrambe direzioni, sia con il segno positivo o negativo.
Operazioni con i Numeri Interi Relativi
I numeri Interi Relativi sono uguali ai Numeri Naturali riguardo alle operazioni. Con i Numeri Interi Relativi possiamo: Sommare, Sottrare, Moltiplicare e Dividere. Vediamo a continuazione ogni una.
Addizione dei numeri Interi Relativi
La somma di due Numeri Interi Relativi si indica con il segno +, fra i Numeri Interi chiusi tra parentesi col proprio segno, Vediamo un esempio.
Se vogliamo sommare +5 e -2: (+5) + (-2)
Dobbiamo distinguere per l’addizione di due Numeri Interi se sono Concordi o Discordi.
Somma di Numeri Interi Relativi Concordi
I Numeri Interi Relativi Concordi sono quelli che hanno lo stesso segno. La somma di due Numeri Interi Relativi Concordi è un numero relativo che ha per segno lo stesso degli addendi e per valore totale la somma dei loro valori assoluti.
Vediamo un esempio: (+4) + (+5) = +9 o (-2) + (-4) = -6
Somma di Numeri Interi Relativi Discordi
I Numeri Interi Relativi Discordi sono quelli che hanno un segno contrario. La somma di due Numeri Interi Relativi Discordi è un numero che ha per segno quello dell’addendo con valore totale maggiore e per valore assoluto la differenza dei valori totali dei numeri stabilito.
Vediamo un esempio: (-5) + (+4) = -1
La Somma di Numeri Interi Relativi opposti e uguale a cero
Vediamo un esempio: (-4) + (+4) = 0
Sottrazione di Numeri Interi Relativi
Come abbiamo già visto e molto importante il segno che troviamo davanti al numero perché ci indica il suo valore. Quando si resta dobbiamo vedere quale segno ha un maggiore e minore valore assoluto, non dobbiamo dimenticare che quando abbiamo due segni che sono uguali diventano il contrario.
Vediamo un esempio: (+4) – (-2 ) = +4 + 2 = 6
Moltiplicazione di Numeri Interi Relativi
Dobbiamo prima moltiplicare i valori assoluti ma ricordiamoci dei segni. Due segni postivi, il risultato e positivo. Due segni negativi, il risultato e positivo. Un segno positivo e negativo, il risultato e negativo.
Vediamo un esempio facile: -3 x 2 = -6
Divisione di Numeri Interi Relativi
Nella divisione dobbiamo fare sempre uguale, ma invece di moltiplicare faremo la divisione.
Vediamo un esempio facile: -6 / 2 = -3
Origine dei Numeri Interi Relativi
I Numeri Interi Relativi ci aiutano a fare operazioni che con i numeri naturali non riusciamo, come per esempio: date storiche prima o dopo la nascita di Gesù o le temperature. I Numeri Interi Relativi sono la risposta a queste limitazioni dei numeri naturali.
La retta numerica, invece, si crede fu creata da John Wallis, uno dei matematici più importanti della storia. John Wallis è stato chi ha dato la vita al calcolo moderno e che definii la funzione del segno infinito.
Possiamo concludere che i Numeri Interi Relativi servono per realizzare operazioni matematiche attraverso le quali sappiamo con esattezza il valore che vogliamo posizionato sia in tempo che spazio.