Vuoi sapere quali sono numeri complessi e a cosa servono?
Continuate a leggere e scoprite tutte le loro proprietà, modi di rappresentarle, storia e tanto altro !
Cosa sono i Numeri Complessi?
I numeri complessi sono di grande importanza in matematica e anche in algebra, tra le altre discipline. Sono numeri che si estendono dai numeri reali formando da soli un gruppo chiuso in termini algebrici. Per la loro designazione si utiliza la lettera C.
Una delle differenze rispetto ai numeri reali sta nel fatto che nel gruppo dei numeri complessi sono incluse le radici dei polinomi senza eccezione. Detto questo, possiamo aggiungere che i numeri complessi possono essere presentati dall’operazione somma di un numero immaginario e anche di un numero reale:
z = a + bi dove i l’unità immaginaria, cioè √(-1)
In questo video trovate una perfetta introduzione ai numeri complessi:
I numeri complessi e la forma trigonometrica
Un numero complesso può essere rappresentato in diversi modi:
- Numero complesso in forma binomiale: z = a + bi
- Numero complesso in forma trigonometrica: z = (cos θ + i sin θ)
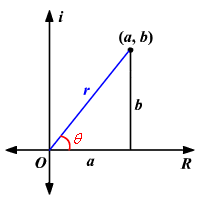
- Numero complesso in forma di coordinate cartesiane: (a, b)
- Numero complesso in forma polare:
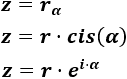
A cosa servono i numeri complessi? Definizione con esempi ed equazioni
Ci sono molte specialità che usano numeri complessi nella loro vita quotidiana, essendo cruciale nell’esecuzione di tutti i tipi di operazioni.
Usato in algebra, equazioni differenziali, analisi, variabili complesse e anche calcolo degli integrali. Sono anche ampiamente utilizzati in aerodinamica, elettromagnetismo, idrodinamica, meccanica quantistica, elettronica, ingegneria, telecomunicazioni, per citare solo alcuni esempi. Sono una risorsa frequente in fisica, ma soprattutto hanno un importanza fondamentale nella matematica.
Un fatto interessante è come i matematici sono a favore dei numeri complessi nella loro preferenza rispetto ai numeri reali. La ragione di questo è che permette loro di risolvere le equazioni con un metodo molto più comodo ed efficiente. Questa situazione può essere spiegata grazie all’esistenza del teorema fondamentale dell’algebra con cui si stabilisce che i numeri complessi rappresentano un gruppo algebricamente chiuso. Altre applicazioni comuni sono le equazioni differenziali, l’analisi complessa e anche l’uso dei frattali.

Possiamo anche aggiungere che i numeri complessi influenzano la geometria con forme e triangoli, equazioni dinamiche, fluidodinamica, relatività e teoria del controllo. Varie scienze hanno tratto grande beneficio dalle scoperte che questi numeri hanno portato.
Storia e Origini dei numeri complessi
Non è sorprendente vedere il nome Erone di Alessandria associato all’invenzione dei numeri complessi, perché non è stato invano uno dei più importanti pensatori del suo tempo. Creatore di invenzioni di ogni tipo, Erone fu anche il primo (secondo i riferimenti storici) a imbattersi in un numero complesso.
Lo fece quando incontrò una sezione impossibile in una piramide. Questo era nel anno I a.C e sarebbe servita come prima manifestazione troppo precoce di ciò che sarebbe venuto molto più tardi.

Dovete saltare nel XVI secolo perché i numeri complessi abbiano una presenza reale nella società. Il nome più importante in questo senso è quello di Girolamo Cardano un matematico italiano che propose la sua accettazione nel 1545 con un trattato sulle equazioni quartiche e cubiche. Ma anche se la sua proposta era piena di logica, la verità è che ciò che Cardano presentò non fu ben accolto.
I matematici contemporanei di Cardano non gli diedero sufficiente validità. Era necessario aspettare il lavoro di Caspar Wessel e Jean-Robert Argand rispettivamente nel 1799 e nel 1806, in modo che le loro teorie fossero effettivamente stabilite.

Successivamente Carl Friedrich Gauss si prese l’incarico di organizzare tutta la conoscenza, facendone una definizione approfondita y también dimostrandone l’empleo nel teorema fondamentale dell’algebra. Già nel XIX secolo è stato implementato con numeri reali a coppie.

La prima volta che si utilizza il termine “numero complesso” fu per mano di Carota nell’anno 1803 dato che Cardano si era precedentemente riferito ad essi come puri numeri negativi. Oggi formano un pilastro cruciale nello studio e nell’esecuzione di operazioni matematiche per le quali sono già indispensabili.
Proprietà dei numeri complessi
Tutti i numeri complessi rientrano nelle caratteristiche proprie che definiscono le leggi relative alla assiomatica. Da questo sappiamo che i numeri complessi hanno proprietà associative, commutative e distributive, oltre al fatto che questi numeri hanno gli inversi additivi e gli inversi moltiplicativi
Apprezziamo, d’altra parte, che non c’è la possibilità di ordinarli e questo è qualcosa in cui differiscono, per esempio, dai numeri reali. Oltre a questo, è possibile generalizzare i numeri complessi, in modo che essi formino il numeri ipercomplessi.
La proprietà più bella di questi numeri complessi sta nel fatto che ci danno la possibilità di per ottenere soluzioni che non sono possibili con i numeri reali all’interno di alcune equazioni date. Così, le equazioni che non possono avere una soluzione reale si trovano con i numeri complessi.
Operazioni con i numeri complessi e formule
L’uso dei numeri complessi viene fatto attraverso diversi tipi di operazioni tra cui la uguaglianza, addizione, scala per prodotto, moltiplicazione, sottrazione o divisione.
- Somma: lo realizzeremo con una elabora basata sulla somma prima di a + bi con c + di che ci darà il risultato (a + c) + (b + d) i.
- Sottrazione: partiremo da a + bi meno c + di con un risultato che radica in (a – c) + (b – d) i.
- Moltiplicazione: avremo a + bi moltiplicato per c + di che risulterà in (ac – bd) + (ad + bc) i.
Per l’uso dei numeri complessi si raccomanda di conoscere la forma polare che porta una semplicità speciale alle operazioni di moltiplicazione. Sono importanti anche le formule di Moivre e di Eulero, che con i loro metodi aiutano a realizzare operazioni e ad ottenere il massimo beneficio da questi numeri in modo applicato.