Se continuate a leggere, imparerete cosa sono, come sono classificati, la sua storia e molto di più!
Cosa sono i numeri reali? Definizione
Noi intendiamo i numeri reali come tutti i gruppi che comprendono i numeri irrazionali, i numeri razionali, i numeri interi e i numeri naturali. Ci sono diversi modi in cui possiamo costruire e descrivere questi numeri a seconda delle circostanze e del rigore matematico da cui partiamo.
Sono stati definiti con l’intenzione di separare questi numeri dal numero immaginario i che ha un valore uguale alla radice quadrata di -1.
Simbolo dei Numeri Reali
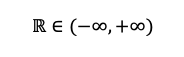
Come posizionare un numero sulla linea reale?
Il retta reale è la linea sulla quale possiamo collocare tutti i numeri reali. Potete vederlo chiaramente con la seguente immagine:

Classificazione dei numeri reali con esempi chiari
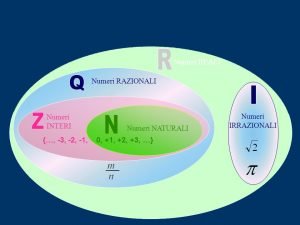
Possiamo dividere i numeri reali in tre blocchi principali:
- Razionali e Irrazionali Anche se si usa la lettera R per nominare l’insieme dei numeri reali, nel caso dei numeri razionali e irrazionali si usano rispettivamente le lettere Q e I. Cosa intendiamo per numeri razionali? Sono tutti quelli che abbiamo la possibilità di rappresentare in base al quoziente di un totale di due interi. Un buon esempio sono ½, 0, 5 o ¾, che allo stesso tempo hanno rappresentazioni decimali periodiche. Spiegare cosa sono gli irrazionali è molto più semplice, questa categoria include assolutamente tutte le altre, che sono quelle che hanno espansioni decimali aperiodiche.
1/4 = 0,25 (razionale)
1/3 = 0,3333… (irrazionale)
- Algebrico e Trascendentale La lettera A è usata per classificare i numeri trascendentali e algebrici. Per conoscere i numeri algebrici dobbiamo tener conto che sono quelli che si presentano quando c’è un polinomio formato da coefficienti razionali in cui è presente. Se non è un numero algebrico, è un numero trascendente. È essenziale capire che, sebbene tutti i numeri razionali siano per definizione algebrici, non tutti quelli algebrici risultano essere numeri razionali.
- Computabile e Irriducibile Infine, quando parliamo di un numero calcolabile? Sono quei numeri che ci permettono di scriverlo in un programma che genererà all’infinito quel numero senza sosta. Cosa succede quando il numero non è calcolabile? In questo caso lo chiamiamo numero irriducibile. I numeri reali calcolabili usano la simbologia Rcomp.
Storia dei numeri reali
Dobbiamo tornare indietro nel tempo per situarci alla nascita dei numeri reali. Anche se il lavoro con i numeri era già iniziato con la mano dei egiziani precedentemente, Pitagora che nel 500 a.C vide la necessità che esisteva per i numeri che oggi conosciamo come irrazionali.
Successivamente l’indiano ha creato i numeri negativi, il cinese li perfezionò, e nel XVIII secolo si usavano i numeri reali, ma non erano veramente definiti con precisione. Colui che aveva il compito di mettere in ordine tutti gli studi e di definirli esattamente era Georg Cantor nell’anno 1871. Ha progettato quella che è conosciuta come la teoria degli insiemi, che comprendeva cardinali infiniti e finiti e incorporazioni successive.
È stato completato dal lavoro di Richard Dedekind. Il loro lavoro congiunto sistematizzò i numeri reali utilizzando le conoscenze di tutti i matematici dall’inizio dei tempi. Questa è conosciuta come una delle più importanti collaborazioni nella ricerca matematica nella storia dell’umanità per il modo in cui i contributi dei matematici di molti secoli prima erano ancora validi nella definizione finale dei numeri reali.
Il risultato, quindi, non è stato solo merito di Georg Cantor o Richard Dedekind, che si sono presi la responsabilità di finire il lavoro con la loro intelligenza, ma hanno anche partecipato: Pitagora, Cartesio, Leibniz, Newton, Gauss, Lagrange o Riemann, tra molti altri.
Proprietà dei numeri reali
- I numeri reali sono integrale il che significa che non ci sono spazi vuoti nelle diverse serie di numeri. Pertanto, gli insiemi che hanno un limite superiore hanno anche un limite inferiore per mantenere la completezza.
- Allo stesso modo, questi numeri sono infinito in entrambe le direzioni e questo vale anche per il modo in cui possono essere espansi di forma decimale all’infinito. È per questo che sono numeri che usiamo comunemente quando calcoliamo il tempo o la lunghezza. Il numero pi greco è un buon esempio di un tale numero, che è infinito e allo stesso tempo scritto in forma decimale.
- Alcune delle caratteristiche che si verificano quando si eseguono operazioni con i numeri reali includono la constatazione che il le somme sono chiuse, associative e commutative. Lo zero non gioca alcun ruolo e se aggiungiamo un numero reale allo zero, ci darà sempre lo stesso numero reale Tutti i numeri reali hanno numeri simmetrici che danno come risultato un totale di 0.
- D’altra parte, il anche le moltiplicazioni sono chiuse, commutative e associative ma l’elemento neutro che ricorre in queste operazioni è quello rappresentato dal numero 1. Infine, dobbiamo sapere che tutti i numeri reali (tranne lo zero) hanno un numero inverso di tipo moltiplicativo.
Lo studio dei numeri reali ha anche una conoscenza approfondita dei numeri naturali, dei numeri interi, dei numeri razionali e dei numeri irrazionali, poiché fanno tutti parte della stessa squadra e della struttura chiave della matematica
Quali operazioni non si possono fare con i numeri reali?
Le operazioni che si possono eseguire con l’uso dei numeri reali è davvero ampia, includendo tutte le operazioni fondamentali de ella matematica, è più produttivo parlare di quelli che non possono essere eseguiti con queste cifre.
- Per esempio, non ci sono divisioni tra il valore zero per il semplice fatto che non esiste un inverso moltiplicativo di questo numero.
- Più in là, non ci sono radici pari comprese sia le radici quadrate che le radici seste o quarte, con l’uso di numeri negativi all’interno dei numeri reali.
- E infine, non c’è possibilità di trovare il logaritmo di un numero reale che è negativo.
Con queste eccezioni dobbiamo sempre fare particolare attenzione nelle operazioni di calcolo per non incorrere in muri difficili da superare, come è successo ad alcuni dei matematici più famosi della storia.